Seite zuletzt aktualisiert: 15.12.2024
Wurzel ziehen
Als Einstiegsbeispiel ziehen wir die dritte Wurzel aus der komplexen Zahl \( 4 + i \cdot 3 \) .
1. Schritt: Umwandlung der Zahl in die Polarform
Im ersten Schritt wandeln wir die Zahl \( 4 + i \cdot 3 \) in die Polarform um. Dies wurde im Teil 2 ausführlich dargestellt.
Das Ergebnis entnehmen wir aus ▸Teil 2 - siehe Term (8):
\( 5 \cdot e^{\hspace{0.1em}i\hspace{0.1em} \cdot 0,6435} \)
2. Schritt: Potenzieren
Wir potenzieren die Polarform mit \( \frac{1}{3} \) :
\( (5 \cdot e^{\hspace{0.1em}i\hspace{0.1em} \cdot 0,6435})^{\frac{1}{3}} \\
= 5^\frac{1}{3} \cdot e^{\hspace{0.1em}i\hspace{0.1em} \cdot 0,6435 \cdot \frac{1}{3}} \\
= 1,71 \cdot e^{\hspace{0.1em}i\hspace{0.1em} \cdot 0,2145}
\)
3. Schritt: Umwandlung des Ergebnisses in die kartesische Form
Um die Polarform wieder in die kartesische Form zurück zu verwandeln, verwendet man die Formeln (1) und (2) aus ▸Teil 2.
\( x = 1,71 \cdot cos\: 0,2145 \)
\( y = 1,71 \cdot sin\: 0,2145 \)
Man erhält somit für die dritte Wurzel:
\( W_1 = 1,71 \cdot cos\: 0,2145 \,+\, i \cdot 1,71 \cdot sin\: 0,2145 \)
\( W_1 = 1,671 + i \cdot 0,364 \) . (1)
Aber Achtung:
Die schlauen Köpfe, die sich vor einigen Jahrhunderten das erste Mal mit dem Phänomen 'Komplexe Zahlen' beschäftigt haben, haben sehr schnell herausgefunden, dass es noch zwei weitere Lösungen gibt!
In der Polarform gibt es für jede komplexe Zahl unendlich viele Darstellungen, weil man zum Winkel \( \varphi \) ein beliebiges Vielfaches von \( 2 \pi \) addieren kann, was zu derselben komplexen Zahl führt. Also:
\( r \cdot e^{\hspace{0.1em}i\hspace{0.1em} (\varphi + 2\pi \cdot k)}\) mit \( k = 0,1,2,3,... \)
Normalerweise wird nur die Grunddarstellung mit \( k = 0 \) gewählt, so dass der Winkel \( \varphi \) immer im Bereich \( 0 \le \varphi < 2\pi \) liegt. Wählt man jedoch die Darstellung mit \( k = 1 \) und potenziert mit \( \frac{1}{3} \) , so erhält man wieder einen Winkel im Bereich \( 0 \le \varphi < 2\pi \) und damit eine zweite Lösung. Verwendet man die Darstellung mit \( k = 2 \) und potenziert mit \( \frac{1}{3} \) , erhält man eine dritte Lösung.
Erst ab \( k = 3 \) wiederholen sich die ersten drei Lösungen.
Berechnung der zweiten Lösung mit \( k = 1 \) :
\( 5^\frac{1}{3} \cdot e^{\hspace{0.1em}i\hspace{0.1em} \cdot (0,6435 + 2\pi \cdot 1) \cdot \frac{1}{3}} \\
= 1,71 \cdot e^{\hspace{0.1em}i\hspace{0.1em} \cdot\hspace{0.1em} 2,3089} \)
Nach Rücktransformation in kartesische Koordinaten erhält man:
\( W_2 = -1,151 + i \cdot 1,265 \) (2)
Berechnung der dritten Lösung mit \( k = 2 \) :
\( 5^\frac{1}{3} \cdot e^{\hspace{0.1em}i\hspace{0.1em} \cdot (0,6435 + 2\pi \cdot 2) \cdot \frac{1}{3}} \\
= 1,71 \cdot e^{\hspace{0.1em}i\hspace{0.1em} \cdot\hspace{0.1em} 4,4033} \)
Nach Rücktransformation in kartesische Koordinaten erhält man:
\( W_3 = -0,520 - i \cdot 1,629 \) (3)
In der folgenden Zeichnung sind die drei Wurzeln \( W_1, W_2 \) und \( W_3 \) grafisch dargestellt.
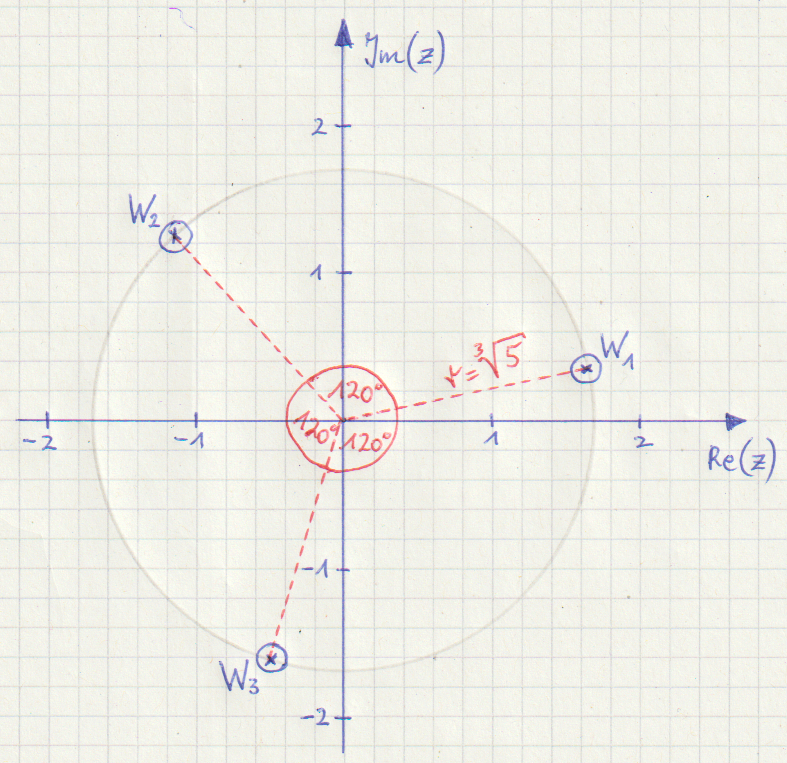
Sie liegen alle auf einem Kreis mit dem Radius \( 5^\frac{1}{3} \) bzw. \( \sqrt[3]{5} \) und ihre Winkel unterscheiden sich um 120°.
Entsprechend hat die fünfte Wurzel fünf verschiedene Lösungen. Hier muss man die Fälle \( k = 0, 1, 2, 3, 4 \) berücksichtigen. Die fünf Lösungen liegen auf einem Kreis mit dem Radius \( \sqrt[5]{5} \) und ihre Winkel unterscheiden sich um 72° (360° : 5 = 72°).
Vergleich mit den Reellen Zahlen
1. Wurzeln
Im Bereich der reellen Zahlen gibt es nur Wurzeln aus positiven Zahlen und das Ergebnis ist immer positiv und eindeutig. Im Bereich der komplexen Zahlen kann die Wurzel aus jeder Zahl gezogen werden. Die Wurzel aus einer komplexen Zahl ist nicht eindeutig. Für Zahlen ungleich null gibt es immer mehrere Wurzeln.
Der Term \( \sqrt[3]{-8} \) zum Beispiel ist im Reellen nicht definiert.
Die Gleichung \( x^3=-8 \) hat nicht die Lösung \( \sqrt[3]{-8} \) , sondern \( -\sqrt[3]{8} \hspace{0.5em} (= -2) \) !
Im Komplexen gibt es drei verschiedene Wurzeln aus -8 (siehe Abschnitt 'Spezielle Wurzeln').
Allgemein gilt für komplexe Zahlen ungleich null:
Für die n-te Wurzel gibt es immer n verschiedene Lösungen.
2. Potenzgesetze
Noch etwas ist im Komplexen unbedingt zu beachten:
Die aus dem Reellen bekannten Potenzgesetze gelten nicht mehr!
Zum Beispiel ist die folgende Termumformung falsch:
\( x^\frac{1}{3} \cdot y^\frac{1}{3} = (x \cdot y)^\frac{1}{3} \)
Schon der erste Faktor \( x^\frac{1}{3} \, (= \sqrt[3]{x}) \) ist nicht eindeutig, sondern hat drei verschiedene mögliche Werte (drei verschiedene dritte Wurzeln). Es wäre gar nicht klar, welche dritte Wurzel des ersten Faktors mit welcher dritten Wurzel des zweiten Faktors hier multipliziert werden soll. Beachtet man dies nicht, produziert man viele Widersprüche. Einer davon ist im ersten Abschnitt in ▸Teil 1 dargestellt.
Spezielle Wurzeln
Im Folgenden sollen einige spezielle Wurzeln betrachtet werden. Mitunter ergeben sich unerwartete Resultate. Und endlich haben diejenigen recht, die behaupten, dass \( \sqrt{4} \) die beiden Lösungen 2 und -2 hat. (Im Reellen ist diese Behauptung falsch. Dort ist nur die 2 eine Lösung.)
Beispiel 1: \( \sqrt[3]{-8} \)
Die Zahl \( -8 \) kann als \( -8 + i \cdot 0 \) geschrieben werden.
Sie wird zunächst in die Polarform transformiert:
\( -8 + i \cdot 0 = 8 \cdot e^{\hspace{0.1em}i\hspace{0.1em} \cdot \pi} \) .
Zum Winkel \( \pi \) wird das k-fache von \( 2\pi \) addiert:
\( 8 \cdot e^{\hspace{0.1em}i\hspace{0.1em} \cdot (\pi + 2\pi \cdot k)} \) mit \( k = 0, 1, 2 \) .
Nun wird mit \( \frac{1}{3} \) potenziert.
1. Lösung (k = 0):
\( 8^{\frac{1}{3}} \cdot e^{\hspace{0.1em}i\hspace{0.1em} \cdot (\pi + 2\pi \cdot 0) \cdot \frac{1}{3}} \\
= 2 \cdot e^{\hspace{0.1em}i\hspace{0.1em} \cdot \frac{\pi}{3}} \\
= 1 + i \cdot \sqrt{3} \)
Hier wurde verwendet, dass \( \cos \frac{\pi}{3} = \frac{1}{2} \) und \( \sin \frac{\pi}{3} = \frac{1}{2} \sqrt{3} \) ist.
2. Lösung (k = 1):
\( 8^{\frac{1}{3}} \cdot e^{\hspace{0.1em}i\hspace{0.1em} \cdot (\pi + 2\pi \cdot 1) \cdot \frac{1}{3}} \\
= 2 \cdot e^{\hspace{0.1em}i\hspace{0.1em} \cdot \pi} \\
= -2 \)
3. Lösung (k = 2):
\( 8^{\frac{1}{3}} \cdot e^{\hspace{0.1em}i\hspace{0.1em} \cdot (\pi + 2\pi \cdot 2) \cdot \frac{1}{3}} \\
= 2 \cdot e^{\hspace{0.1em}i\hspace{0.1em} \cdot \frac{5}{3}\pi} \\
= 1 - i \cdot \sqrt{3} \)
Hier wurde verwendet, dass \( \cos \frac{5}{3}\pi = \frac{1}{2} \) und \( \sin \frac{5}{3}\pi = - \frac{1}{2} \sqrt{3} \) ist.
Beispiel 2: \( \sqrt[3]{1} \) (die dritten Einheitswurzeln)
Die Zahl \( 1 \) kann als \( 1 + i \cdot 0 \) geschrieben werden.
Sie wird zunächst in die Polarform transformiert:
\( 1 + i \cdot 0 = 1 \cdot e^{\hspace{0.1em}i\hspace{0.1em} \cdot 0} \) .
Zum Winkel \( 0 \) wird das k-fache von \( 2\pi \) addiert:
\( 1 \cdot e^{\hspace{0.1em}i\hspace{0.1em} \cdot (0 + 2\pi \cdot k)} \) mit \( k = 0, 1, 2 \) .
Nun wird mit \( \frac{1}{3} \) potenziert.
1. Lösung (k = 0):
\( 1^{\frac{1}{3}} \cdot e^{\hspace{0.1em}i\hspace{0.1em} \cdot (0 + 2\pi \cdot 0) \cdot \frac{1}{3}} \\
= 1 \cdot e^{\hspace{0.1em}i\hspace{0.1em} \cdot 0} \\
= 1 \)
2. Lösung (k = 1):
\( 1^{\frac{1}{3}} \cdot e^{\hspace{0.1em}i\hspace{0.1em} \cdot (0 + 2\pi \cdot 1) \cdot \frac{1}{3}} \\
= 1 \cdot e^{\hspace{0.1em}i\hspace{0.1em} \cdot \frac{2}{3}\pi} \\
= -\frac{1}{2} + i \cdot \frac{1}{2}\sqrt{3} \)
Hier wurde verwendet, dass \( \cos \frac{2}{3}\pi = -\frac{1}{2} \) und \( \sin \frac{2}{3}\pi = \frac{1}{2} \sqrt{3} \) ist.
\( 1^{\frac{1}{3}} \cdot e^{\hspace{0.1em}i\hspace{0.1em} \cdot (0 + 2\pi \cdot 2) \cdot \frac{1}{3}} \\ = 1 \cdot e^{\hspace{0.1em}i\hspace{0.1em} \cdot \frac{4}{3}\pi} \\ = -\frac{1}{2} - i \cdot \frac{1}{2}\sqrt{3} \) Hier wurde verwendet, dass \( \cos \frac{4}{3}\pi = -\frac{1}{2} \) und \( \sin \frac{4}{3}\pi = -\frac{1}{2} \sqrt{3} \) ist.
Die dritten Einheitswurzeln
Die in Beispiel 2 berechneten Wurzeln werden als "dritte Einheitswurzeln" bezeichnet. Sie spielen eine große Rolle bei der Lösung kubischer Gleichungen (Gleichungen dritten Grades) mit Hilfe der Cardanischen Formeln. Sie werden häufig mit dem griechischen Buchstaben \( \epsilon \) bezeichnet:
\( \epsilon_1 = 1 \)
\( \epsilon_2 = -\frac{1}{2} + i \cdot \frac{1}{2}\sqrt{3} \)
\( \epsilon_3 = -\frac{1}{2} - i \cdot \frac{1}{2}\sqrt{3} \)
In polarer Form sehen die dritten Einheitswurzeln so aus:
\( \epsilon_1 = 1 \cdot e^{\hspace{0.1em}i\hspace{0.1em} \cdot 0} \)
\( \epsilon_2 = 1 \cdot e^{\hspace{0.1em}i\hspace{0.1em} \cdot \frac{2}{3}\pi} \)
\( \epsilon_3 = 1 \cdot e^{\hspace{0.1em}i\hspace{0.1em} \cdot \frac{4}{3}\pi} \)
Es gilt: \( \epsilon_3 = \bar{\epsilon_2} \) und \( \epsilon_2 = \bar{\epsilon_3} \) (\( \epsilon_2 \) und \( \epsilon_3 \) sind konjugiert komplex zueinander).
Außerdem gilt: \( \epsilon_3 = \epsilon_2^{\,2} \) und \( \epsilon_2 = \epsilon_3^{\,2} \) .
Deshalb bezeichnet man das \( \epsilon_2 \) auch gerne nur mit \( \epsilon \) und das \( \epsilon_3 \) mit \( \epsilon^2 \) .
Die drei Einheitswurzeln wären dann \( 1 \) , \( \epsilon \) , \( \epsilon^2 \) mit \( \epsilon = -\frac{1}{2} + i \cdot \frac{1}{2}\sqrt{3} \) .
Beispiel 3: \( \sqrt[4]{1} \)
Die Zahl \( 1 \) kann als \( 1 + i \cdot 0 \) geschrieben werden.
Die ersten vier Darstellungen in Polarform:
\( 1 \cdot e^{\hspace{0.1em}i\hspace{0.1em} \cdot (0 + 2\pi \cdot k)} \) mit \( k = 0, 1, 2, 3 \) .
1. Lösung (k = 0):
\( 1^{\frac{1}{4}} \cdot e^{\hspace{0.1em}i\hspace{0.1em} \cdot (0 + 2\pi \cdot 0) \cdot \frac{1}{4}} \\
= 1 \cdot e^{\hspace{0.1em}i\hspace{0.1em} \cdot 0} \\
= 1 \)
2. Lösung (k = 1):
\( 1^{\frac{1}{4}} \cdot e^{\hspace{0.1em}i\hspace{0.1em} \cdot (0 + 2\pi \cdot 1) \cdot \frac{1}{4}} \\
= 1 \cdot e^{\hspace{0.1em}i\hspace{0.1em} \cdot \frac{\pi}{2}} \\
= i \)
3. Lösung (k = 2):
\( 1^{\frac{1}{4}} \cdot e^{\hspace{0.1em}i\hspace{0.1em} \cdot (0 + 2\pi \cdot 2) \cdot \frac{1}{4}} \\
= 1 \cdot e^{\hspace{0.1em}i\hspace{0.1em} \cdot \pi} \\
= -1 \)
4. Lösung (k = 3):
\( 1^{\frac{1}{4}} \cdot e^{\hspace{0.1em}i\hspace{0.1em} \cdot (0 + 2\pi \cdot 3) \cdot \frac{1}{4}} \\
= 1 \cdot e^{\hspace{0.1em}i\hspace{0.1em} \cdot \frac{3}{2}\pi} \\
= -i \)
Beispiel 4: \( \sqrt{-1} \)
Die Zahl \( -1 \) kann als \( -1 + i \cdot 0 \) geschrieben werden.
Die ersten zwei Darstellungen in Polarform:
\( 1 \cdot e^{\hspace{0.1em}i\hspace{0.1em} \cdot (\pi + 2\pi \cdot k)} \) mit \( k = 0, 1 \) .
1. Lösung (k = 0):
\( 1^{\frac{1}{2}} \cdot e^{\hspace{0.1em}i\hspace{0.1em} \cdot (\pi + 2\pi \cdot 0) \cdot \frac{1}{2}} \\
= 1 \cdot e^{\hspace{0.1em}i\hspace{0.1em} \cdot \frac{\pi}{2}} \\
= i \)
2. Lösung (k = 1):
\( 1^{\frac{1}{2}} \cdot e^{\hspace{0.1em}i\hspace{0.1em} \cdot (\pi + 2\pi \cdot 1) \cdot \frac{1}{2}} \\
= 1 \cdot e^{\hspace{0.1em}i\hspace{0.1em} \cdot \frac{3}{2}\pi} \\
= -i \)
Beispiel 5: \( \sqrt{i} \)
Die Zahl \( i \) kann als \( 0 + i \cdot 1 \) geschrieben werden.
Die ersten zwei Darstellungen in Polarform:
\( 1 \cdot e^{\hspace{0.1em}i\hspace{0.1em} \cdot (\frac{\pi}{2} + 2\pi \cdot k)} \) mit \( k = 0, 1 \) .
1. Lösung (k = 0):
\( 1^{\frac{1}{2}} \cdot e^{\hspace{0.1em}i\hspace{0.1em} \cdot (\frac{\pi}{2} + 2\pi \cdot 0) \cdot \frac{1}{2}} \\
= 1 \cdot e^{\hspace{0.1em}i\hspace{0.1em} \cdot \frac{\pi}{4}} \\
= \frac{1}{2} \sqrt{2} + i \cdot \frac{1}{2} \sqrt{2} \)
Hier wurde verwendet, dass \( \cos \frac{\pi}{4} = \sin \frac{\pi}{4} = \frac{1}{2} \sqrt{2} \) ist.
2. Lösung (k = 1):
\( 1^{\frac{1}{2}} \cdot e^{\hspace{0.1em}i\hspace{0.1em} \cdot (\frac{\pi}{2} + 2\pi \cdot 1) \cdot \frac{1}{2}} \\
= 1 \cdot e^{\hspace{0.1em}i\hspace{0.1em} \cdot \frac{5}{4}\pi} \\
= -\frac{1}{2} \sqrt{2} - i \cdot \frac{1}{2} \sqrt{2} \)
Hier wurde verwendet, dass \( \cos \frac{5}{4}\pi = \sin \frac{5}{4}\pi = - \frac{1}{2} \sqrt{2} \) ist.
Quadratwurzeln allgemein:
An den Beispielen 4 und 5 sieht man, dass für die beiden Quadratwurzeln \( w_1 \) und \( w_2 \) gilt:
\( w_2 = -w_1 \) .
Dies muss für alle Quadratwurzeln einer komplexen Zahl \( z \) gelten, denn wenn \( w_1\hspace{0.01em}^2 = z \) ist, dann muss zwangsläufig auch \( (-w_1)^2 = z \) sein. Da es bei komplexen Zahlen (ungleich null) immer genau zwei Quadratwurzeln gibt, können nur \( w_1 \) und \( -w_1 \) die beiden Quadratwurzeln sein.